| EXCALIBUR Adaptive Constraint-Based Agents in Artificial Environments |
| [REALIZATION] | [Action Resource Constraints] [Task Constraints] |
| [ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ] |
(Related publications: [PUBLink] [PUBLink])
An ARC is connected to a set of pairs P and two variables c and h. A pair of the set P, (si, ei), represents a task i that uses the machine/resource. The starting time of a task i is represented by the variable si and the end of the task by the variable ei. The ARC's role is to prevent overlapping tasks. For each discrete point of time from c to h, the number of assigned tasks - 1 is added to the constraint's inconsistency if there is an assignment of more than one task at this time point. The constraint can change the tasks' temporal distribution by changing the variables si/ei.
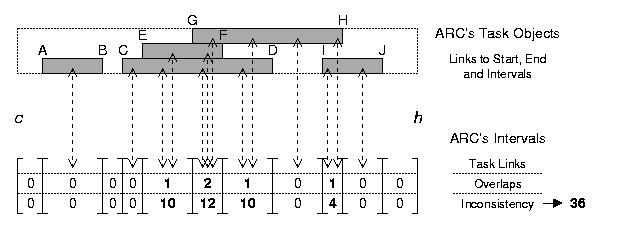
An ARC's basic internal structures are a set of task objects and a multiple-linked list of temporal intervals. A task object contains references to the start variable, the end variable and its intervals. The intervals split the time from c to h into maximal parts such that each interval has the same task assignment for its duration (see figure below). Task overlaps are mapped to the intervals, and the inconsistency of an interval is computed by the overlaps multiplied by the interval's length. Links to an interval's task objects are also stored. The ARC's total inconsistency is the sum of the intervals' inconsistencies.

The ARC's basic heuristic (ARC-H1) selects an inconsistent interval (i1; see selection a) of the figure below) with a choice probability for an interval that is proportional to the interval's inconsistency. For example, if the intervals A to E have inconsistencies of Acosts = 10, Bcosts = 12, Ccosts = 10, Dcosts = 0 and Ecosts = 4, the chance of being chosen is 27.8% for A, 33.3% for B, 27.8% for C, 0% for D and 11.1% for E.
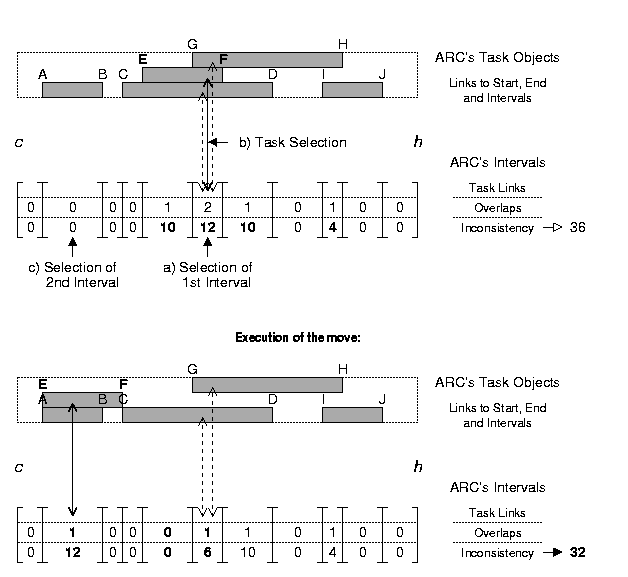
Then, one of the interval's tasks (t1) is chosen at random. The task's start variable is shifted to the beginning of an interval i2, a choice probability for the interval being proportional to its length times its task-number improvement with respect to the interval i1. Only intervals with fewer tasks than the i1 interval's (without the task t1) are considered for this decision, and the maximal length of intervals considered for the multiplication is that of the task t1.
| [REALIZATION] | [Action Resource Constraints] [Task Constraints] |
For questions, comments or suggestions, please contact us.
Last update:
May 19, 2001 by Alexander Nareyek