| EXCALIBUR Adaptive Constraint-Based Agents in Artificial Environments |
| [DOCUMENTATION] | [Preface] [Introduction] [Local] [SCSP] [Model] [Application] [Conclusion] |
| [ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ] |
(Related publication: [PUBLink])
In an environment that is only partially observable for an agent, it is not clear which objects exist, i.e., how many variables and resources of which kind are available. The closed-world assumption cannot be applied and we cannot restrict the planning process to a given set of state variables.
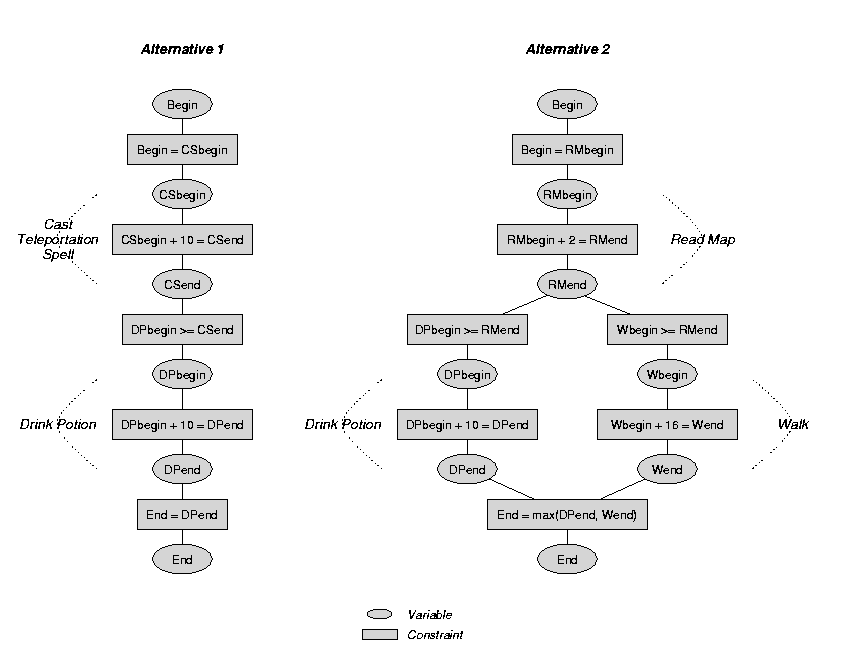
Furthermore, for a planning problem (and many other problem domains), numerous alternative structures are potentially valid for realizing a solution to a problem. The figure below gives an example of two alternatives/CSPs. The wizard can either cast a teleportation spell to get to a Halloween party and drink a magic potion to give himself an appropriate appearance for the party after he is teleported, or consult a map and walk while drinking the potion. This example shows that there are options not only with respect to the assignment of variables, but also to the graph structure (number and connection of the variables and constraints) itself.

Conventional constraint satisfaction is unable to handle structural alternatives, as constraint satisfaction problem formulations are static. There is a given set of constraints and variables, and the specified structure does not change. For the task of generating a plan, though, there are alternative CSP structures and the search for the structure of the CSP must be part of the satisfaction process - a structural constraint satisfaction problem (SCSP).
The structural constraint satisfaction problem should not be confused with the dynamic constraint satisfaction problem (see [PUBLink] for a brief survey). Dynamic constraint satisfaction tries to revise a variable assignment with given changes to the constraint graph and does not include graph changes as part of the search.
In contrast to constructive approaches for building a graph, an SCSP adopts the constraint programming approach and defines solutions by specifying correctness tests. These test - so-called structural constraints - are restrictions on admissible constraint graphs. The basic satisfaction idea is to iteratively change a graph (starting with an empty graph) based on an algebraic graph grammar, which is generically produced using the problem definition.
The presentation of the SCSP approach will be done by way of an example of an extended job-shop scheduling scenario, where a task can be executed with an arbitrary number of breaks in between. It is hardly possible to express this with a conventional CSP because the formulation would require a variable number of variables for the subtasks' start times and durations as well as a variable number of constraints.
Section [Algebraic Graph Grammars] gives a brief introduction in graph grammars. This concept is extended by structural constraints in Section [Structural Constraints]. The extension is used in Section [Structural Constraint Satisfaction Problems] to formulate structural constraint satisfaction problems. Sections [Generating the Search Space] and [Avoiding Redundancy] show how to use the SCSP formulation to generically create a graph grammar with additional structural constraints to prevent from redundancies. The concept of structural constraint satisfaction is combined with the previous chapter's approach of global constraints for local search in Section [Combination with the Global Constraint Approach].
| [DOCUMENTATION] | [Preface] [Introduction] [Local] [SCSP] [Model] [Application] [Conclusion] |
For questions, comments or suggestions, please contact us.
Last update:
January 31, 2002 by Alexander Nareyek