[ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ]

(Related publications: [PUBLink] [PUBLink] [PUBLink])

A solution to an SCSP is a constraint graph with an arbitrary number of variables, conventional (or object) constraints and connecting edges, such that the graph satisfies all structural constraints. Thus, the basic ingredients to formulate an SCSP are a set of types of conventional (or object) constraints and a set of structural constraints. But in most cases there will be much less allowed constellations of conventional (or object) constraints than inconsistent ones. This means that - at least for the direct neighborhood of a constraint - a constructive specification is more appropriate than a huge number of structural constraints. Because of this, our SCSP specification will include generic constellations alternatives for the direct embedding of a conventional (or object) constraint and minima and maxima for the direct embedding of extensible constraints. This is comparable with conventional CSPs, where a variable's domain is also mostly represented by enumeration mechanisms with minima and maxima instead of constraints.

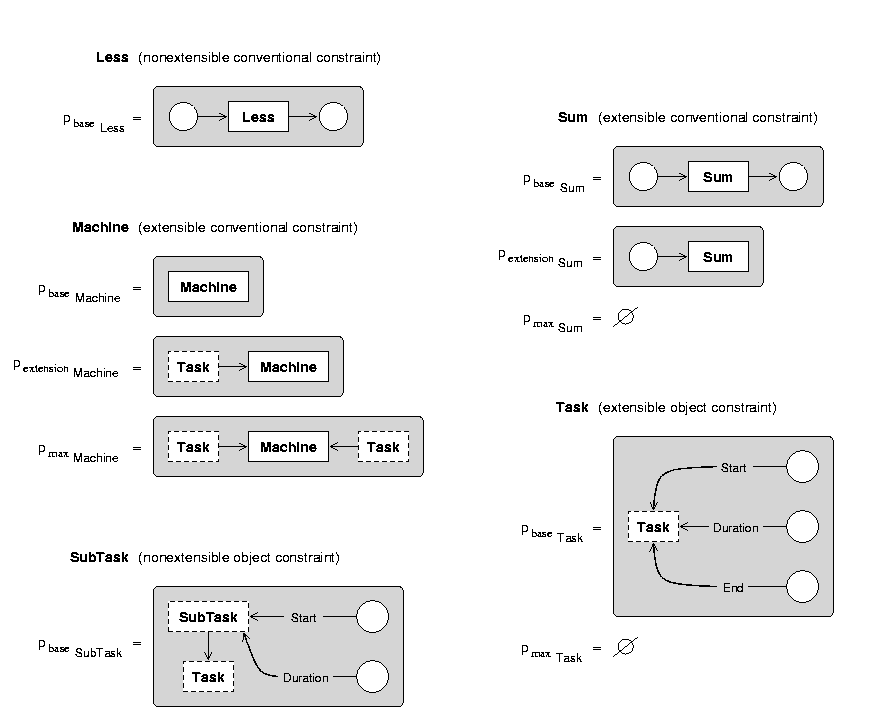
A structural constraint satisfaction problem SCSP = (CD, S) consists of a tuple of sets of constraint descriptions CD = (C_n, C_e, O_n, O_e) and a set of structural constraints S. The constraint descriptions of C_n and O_n are pairs (c, p_base) with a nonextensible conventional (or object) constraint c and its embedding graph p_base. The constraint descriptions of C_e and O_e are 4-tupel (c, p_base, E, p_max) with an extensible conventional (or object) constraint c, its minimal embedding graph p_base, a set of extension graphs E, and the constraint's maximal embedding graph p_max.

An embedding graph shows the constraint with all its directly connected neighbor vertices. If an extensible constraint has no maximal embedding, p_max is the empty graph. An extension graph shows the constraint connected to the vertices that can be added in one step. The figure below shows the residual components of the example SCSP. To show the effects of maximal embedding graphs, we introduce a maximum of two Tasks for a Machine.

There are some requirements that are induced by the construction of the search space in the following section (fulfilled for the presented example SCSP):

• Nonextensible constraints are not allowed to appear in graphs of other constraints, as the addition and deletion productions of constraints partly incorporate their graphs (to satisfy req_ne).
• Constraint-usage cycles are not allowed for the p_base graphs of extensible constraints, e.g., that p_baseA includes a B constraint and p_baseB includes the A constraint (to satisfy req_e).
• If the p_max graph of an extensible constraint is non-empty, no sequence of productions that is applied to the constraint's p_base graph can produce a graph that includes the p_max graph without previously producing the p_max graph (to satisfy req_max).

These requirements can be relaxed by using more sophisticated ways to generate the search space. However, this is not necessary for the work presented here.

For questions, comments or suggestions, please contact us.

Last update:
May 20, 2001 by Alexander Nareyek